Доказать, что прямая, симметричная с медианой относительно биссектрисы внутреннего угла треугольника, делит противоположную сторону на части, пропорциональные квадратам прилежащих сторон.

В треугольнике ABC пусть BD — биссектриса, ВМ — медиана и BN — прямая, симметричная с ВМ относительно BD.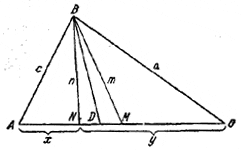

Если S_ABN и S_MBC — площади соответствующих треугольников, то

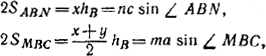
где h_B— высота, опущенная из вершины В на АС.

Так как ∠ABN = ∠МВС, то отсюда

(1)

Аналогично

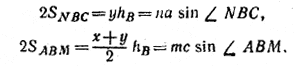
Так как ∠NВС = ∠ABM, то отсюда

(2)

Поделив почленно (1) и (2), получим:

что и требовалось доказать.