Доказать, что сумма квадратов расстояний какой-нибудь точки окружности до вершин правильного вписанного треугольника есть величина постоянная, не зависящая от положения точки на окружности.

Пусть ABC — правильный треугольник со стороной а и r₁, r₂, r₃ — расстояния от точки М описанной окружности до вершин треугольника.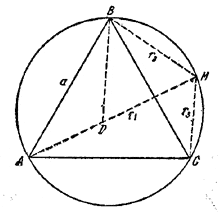

Сначала заметим, что при указанном на рис. положении точки М будет

r₁ = r₂ + r₃

Действительно, если отложить DM = r₂, то получится равносторонний треугольник BMD.

Отсюда следует, что ∠ABD= ∠СВМ, в силу чего \(\Delta\)ABD = \(\Delta\)CBM, так что AD = r₃. Применив к \(\Delta\)ВМС теорему косинусов, получим:

a² = r₂² + r₃² — 2r₂ r₃ cos 120° = r₂² + r₃² + r₂ r₃

Следовательно,

r₁²+ r₂² + r₃²= (r₂ + r₃)² + r₂² + r₃²= 2(r₂² + r₃² + r₂ r₃) = 2a².