Доказать, что если окружность касается изнутри трех сторон четырехугольника и пересекает четвертую сторону, то сумма этой последней и противоположной стороны больше суммы двух других сторон четырехугольника.

Пусть сторона AB четырехугольника ABCD пересекает окружность, а стороны BC, CD, DA касаются ее в точках E, F, G.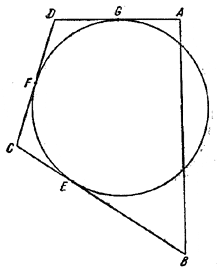

Так как CE = CF и DF = DG, то неравенство

AB + CD > BC + DA

равносильно неравенству

AE > BE + AG,

а это неравенство доказано в решении задачи 189.