Доказать, что если две точки лежат вне окружности и прямая, их соединяющая, не пересекает окружности, то расстояние между этими двумя точками больше разности длин касательных к окружности, проведенных из данных точек, и меньше суммы их. Показать, что одно или другое из этих неравенств не будет выполнено, если прямая пересекает окружность.

Если прямая, соединяющая точки А и В, не пересекает данной окружности, то касательные АС и BD можно провести, так, что точка их пересечения М будет лежать на отрезках АС и BD.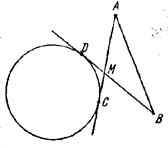

В \(\Delta\)AMВ имеем:

АМ + ВМ > АВ > |AM — BM|,

и так как

АС > AM, BD > BM, MC = MD,

то

AC + BD > АВ > |AC — BD|.

Если прямая AB пересекает окружность, то возможны два случая:

а) хорда, отсекаемая окружностью на прямой АВ, лежит на отрезке АВ;

б) эта хорда лежит вне отрезка АВ.

В случае а) (рис. 108)

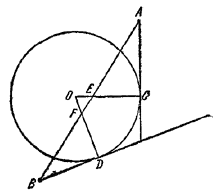
Pис. 108

имеем:

АВ > AE + BF > AC + BD,

так как гипотенузы АЕ, BF в прямоугольных треугольниках AЕС и BFD больше катетов АС и BD.

В случае б) отрезок АВ лежит внутри угла САС' (рис. 109).

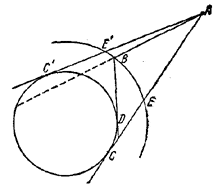
Pис. 109

Проведем через В окружность, концентрическую с данной. Пусть она пересечет АС и АС' в точках Е и E'. Тогда EC = BD и АЕ > АВ. Следовательно,

АВ < AЕ = AС — ЕС = АС — BD.