Через середину С произвольной хорды AB окружности проведены две хорды KL и MN (К и M находятся по одну сторону от AB), Q — точка пересечения AB и KN, P — точка пересечения AB и ML. Доказать, что QC = CP.
Введем обозначения: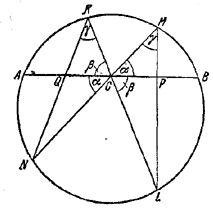
∠PCM = ∠QCN = α, ∠NML = ∠NKL = γ, ∠LCP = ∠QCK = β,
QC = x, PC = y, AC = CB = a.
По теореме об отрезках пересекающихся хорд окружности
NQ • QK = AQ • QB = a2 — x2.
Применяя теорему синусов к треугольникам NQC и QCK, получаем:
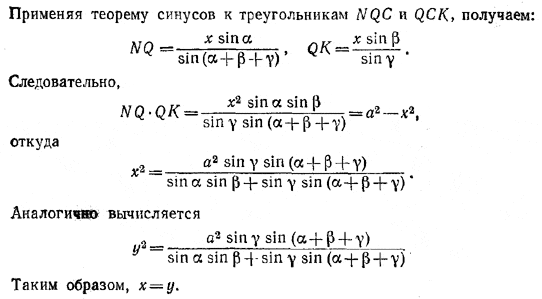
Похожие примеры: