Доказать, что если из концов диаметра круга провести две пересекающиеся хорды, то сумма произведений каждой хорды на ее отрезок от конца диаметра до точки пересечения есть величина постоянная.

Пусть AB — диаметр круга и E — точка пересечения хорд AD и BC.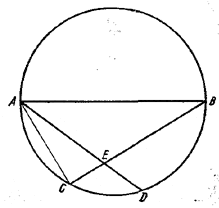

Имеем:

AE • AD = AE² + AE • ED = AС² + EС² + AE • ED.

По свойству пересекающихся хорд

AE • ED = BE • EC.

Поэтому

AE • AD = AC² + EC² + BE • EC = AC² + EC • BC = АС² + (BC — BE) BC = АС² + BC² — BE • BC,

или окончательно

AE • AD + BE • BC = AB².