Доказать, что если разделить хорду окружности на три равные части и соединить с центром окружности концы хорды и точки деления, то соответствующий центральный угол разделится на три части, одна из которых больше двух других.

Пусть AC = CD = DB.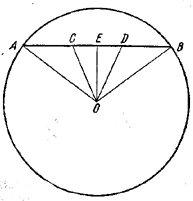

Проведем OE ⊥ AB. Тогда OE — высота, а ОС — медиана в \(\Delta\)AOD. Так как биссектриса ∠AOD лежит между медианой и высотой (см. задачу 150), то

∠AOC < ∠COD.