Доказать, что сумма квадратов длин двух взаимно перпендикулярных пересекающихся хорд окружности больше квадрата ее диаметра, а сумма квадратов отрезков, на которые точка пересечения делит хорды, равна квадрату диаметра.

Пусть М — точка пересечения взаимно перпендикулярных хорд АВ и CD.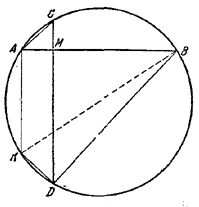

Проведем АК || CD, тогда ВК, — диаметр, АК < CD и

ВК² = АВ² + АК² < AВ² + СD².

Далее, KD = AC, так что

КВ² = ВD² + KD² = ВМ² + DM² + AМ² + СМ².