Из двух точек прямой проведены по две касательные к окружности. В образованные углы с вершинами в этих точках вписаны окружности равного радиуса. Доказать, что их линия центров параллельна данной прямой.

Пусть А, В — данные точки, О — центр данной окружности, R — радиус данной окружности и r — радиус равных вписанных окружностей с центрами О₁ и О₂.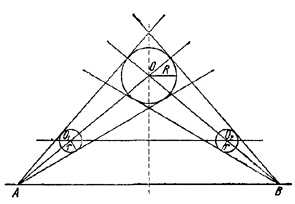

Тогда

Взяв производную пропорцию, получим:

Следовательно, O₁O₂ || АВ.