Доказать, что если диаметр полукруга разделить на две произвольные части и на каждой из них описать полукруг внутри данного полукруга, то площадь, заключенная между тремя полуокружностями, будет равна площади круга, диаметр которого равен длине перпендикуляра, восставленного внутри исходного полукруга из точки деления его диаметра.

Пусть r₁ и r₂ — радиусы полуокружностей, вписанных в данную полуокружность радиуса R.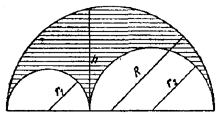

Так как R = r₁ + r₂, то заштрихованная площадь равна

Но

h² = 2r₁ • 2r₂ = 4r₁r₂.

Следовательно,

S = ¹/₄πh²