Внутри равностороннего треугольника со стороной а расположены три равных круга, касающиеся сторон треугольника и взаимно касающиеся друг друга. Найти площадь криволинейного треугольника, образованного дугами взаимно касающихся кругов (вершинами служат точки взаимного касания).
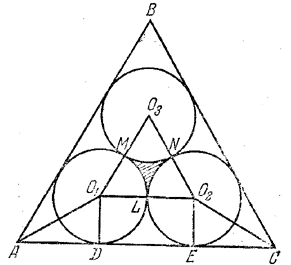
Искомая площадь LМN (заштрихована на рис.) получается, если из площади треугольника О1О2О3 вычесть общую площадь трех секторов O1ML, O2LN и O3NM (их общая площадь равна площади полукруга радиуса r).
Сторона треугольника О1О2О3 равна ![]() (см. предыдущую задачу); поэтому
(см. предыдущую задачу); поэтому
![]()
Общая площадь трех секторов равна
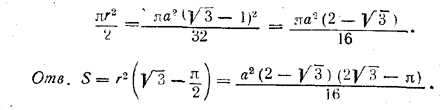
Похожие примеры: