Найти отношение площади треугольника ABC к площади другого треугольника, стороны которого равны медианам треугольника ABC.

Пусть О — точка пересечения медиан в \(\Delta\)ABC (рис.).

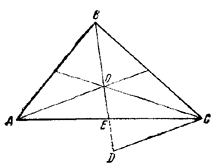
На продолжении медианы BE отложим ED = OE. По свойству медиан стороны \(\Delta\)CDO равны ²/₃сторон треугольника, составленного из медиан. Обозначив площадь последнего через S₁будем иметь:

S₁ = ⁹/₄ S_CDO

С другой стороны, \(\Delta\)CDO составлен из двух, а \(\Delta\)ABC— из шести треугольников, равновеликих \(\Delta\)СЕО. Поэтому S_CDO = ¹/₃S_ABC Следовательно,