Найти третью сторону треугольника, если даны две стороны его а и b и известно, что медианы, соответствующие этим сторонам, пересекаются под прямым углом.
При каких условиях такой треугольник существует?

В треугольнике ABC (рис. 10) О есть точка пересечения медиан AD и BE; AC = b, ВС = а. Найдем АВ = с.

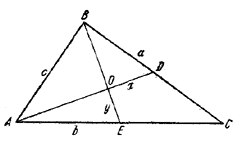
Рис. 10.

Пусть OD = x; ОЕ = у. Используя свойство медиан, из треугольников АОВ, BOD и АОЕ найдем:

Исключив х и у, получим:

Условия существования треугольника со сторонами а, b, с принимают вид

5 (а + b)² > а² + b², 5 (а — b)² < а² + b².

Первое неравенство, очевидно, выполнено при любых а и b, а второе преобразуется в следующее:

а² — ⁵/₂ ab + b²< 0.

Решив это неравенство относительно ^a/_b , окончательно получим:

¹/₂ < ^a/_b< 2