Угол при вершине треугольника, боковые стороны которого равны а и b (a < b), разделен на три равные части прямыми, отрезки которых внутри треугольника относятся как m : n (m < n). Найти длины этих отрезков.
Пусть / AСD = / DCE = / EСВ = α и СЕ = х, CD = y (рис.).
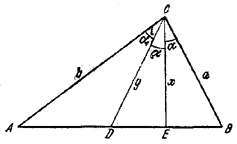
Для площади треугольника ABC можно написать следующие три выражения:
SACD+ SDCB = 1/2 by sin α+ 1/2ay sin 2α,
SACЕ + SЕCB= 1/2bx sin 2α + 1/2ax sin α,
SACD + SDCЕ+ SЕCB= 1/2 by sin α+1/2xу sin α + 1/2ax sin α.
Приравнивая друг другу левые части этих равенств и учитывая условие задачи, придем к системе трех уравнений:
2a cos α= х + а x/y,
2b cos α= y + b y/x,
x/y = m/n
Решив ее, получим:
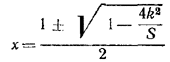
Похожие примеры: