Из точки сферы радиуса R проведены три равные хорды под углом α друг к другу. Определить длину этих хорд.
Пусть О - центр сферы, а AS, BS и CS - данные хорды. Очевидно, что треугольник ABC равносторонний.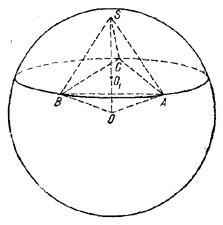
Легко видеть также, что перпендикуляр SO1 на плоскость ABC при продолжении проходит через центр сферы О, так как точка O1 является центром круга, описанного около \(\Delta\)ABC.
Обозначим после этих замечаний через d искомую длину хорд. Из треугольника SAB находим:
АВ = 2d sin α/2
и, следовательно,
![]()
Вычисляя двумя способами площадь равнобедренного треугольника SOA, получаем:
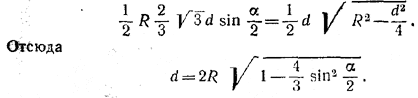
Похожие примеры: