В треугольной пирамиде SABC ребра SA, SC и SB попарно перпендикулярны, АВ = ВС = a, BS = b. Найти радиус вписанного в пирамиду шара.
Радиус вписанного шара rмы найдем по формуле (ср. формулу (1) в решении задачи 240)r = 3V/S
где V-объем пирамиды, a S - ее полная поверхность.
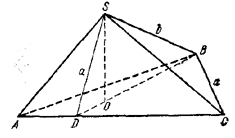
Найдем сначала объем пирамиды. Заметим для этого, что прямоугольные треугольники BSC и BSA равны по равным гипотенузам и общему катету. Ввиду этого прямоугольный треугольник ASC является равнобедренным. Так как
AS = CS = √a2- b2,
то, следовательно,
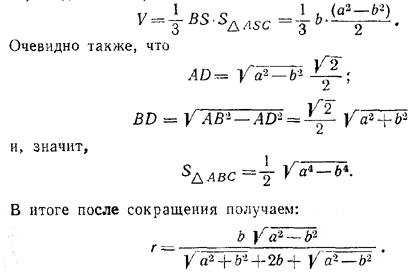
Похожие примеры: