Найти геометрическое место точек, из которых можно провести к данному шару радиуса R три касательные, образующие трехгранный угол с тремя прямыми плоскими углами.
Докажем, что искомое геометрическое место есть сфера радиуса R√6/2 и что центр этой сферы совпадает с центром данной сферы.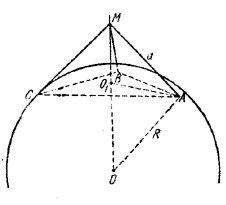
Пусть М - произвольная точка искомого геометрического места; отрезки MA, MB и МС (рис.), будучи отрезками касательных, проведенных к сфере из одной общей точки, равны между собой. Поэтому прямоугольные треугольники АМС, СМВ и АМВ равны. Следовательно, \(\Delta\)ABC равносторонний. Очевидно, что отрезок ОМ пересечет его в центре тяжести О1.
Пусть AM= a, тогда АС = a √2 и АО1 = a√6/3 . Подставляя эти значения в равенствоOM•AO1 = OA•AM (мы пользуемся здесь тем, что \(\Delta\)ОAM прямоугольный, и записываем двумя способами его площадь), получим:
ОM • a √6/3= Ra
Отсюда
OM = √6/2 R
Таким образом, точка М лежит на указанной выше сфере. Вращая данный шар вместе с касательными AM, СМ и ВМ вокруг центра О, мы убедимся в том, что любая точка сферы принадлежит рассматриваемому геометрическому месту.