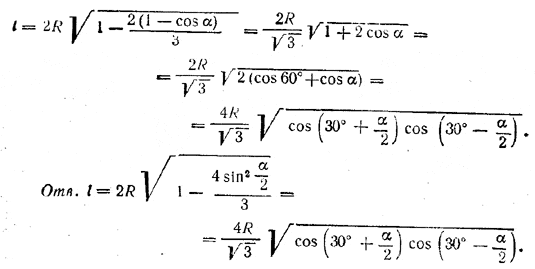В шаре радиуса R из точки его поверхности проведены три равные хорды под углом α друг к другу. Определить их длину.

Обозначим длину равных хорд DA, DB, DC (рис.) через l .

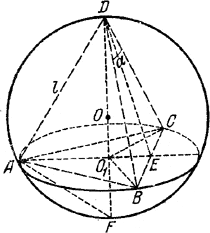
Из равнобедренного треугольника DBC находим BС = 2l sin ^α/₂. Так же найдем, что АВ=AС=2l sin ^α/₂. Следовательно, треугольник ABC- равносторонний.

Опустив перпендикуляр DO₁ на плоскость ABC и установив равенство треугольников DO₁A, DО₁В, DO₁C докажем, что AO₁ = BO₁ = CO₁, т. е. что O₁ есть центр основания (так что пирамида DABC- правильная). Так как точки А, В, С лежат на поверхности шара, то ОА = ОВ = ОС (О - центр шара)- Опустив перпендикуляр из О на плоскость ABC, докажем, что основание перпендикуляра есть центр треугольника ABC, т. е. совпадает с точкой O₁. Следовательно, OO₁ (и, значит, DO₁) лежит на диаметре шара (DF на рис.).

Из прямоугольного треугольника DAF, где DF=2R, находим l² = DA² = 2R•DO₁. Отрезок DO₁ можно связать с l еше одним соотношением. Именно,

Преобразуем это выражение к виду, удобному для логарифмирования. Имеем