В точке А, находящейся на расстоянии а от центра круглого биллиарда радиуса R, лежит упругий шарик, размерами которого можно пренебречь. В какую точку В борта нужно его направить, чтобы, дважды отразившись от борта, он снова вернулся в точку А?

Пусть О — центр биллиарда, В — первая точка отражения и С — вторая точка отражения.
Докажем, что если ∠ABC \(\ne\) 0, то \(\Delta\)ABC равнобедренный.

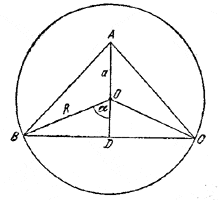
Действительно, \(\Delta\)ВОС равнобедренный, значит, ∠ОВС = ∠ОСВ. По закону отражения (угол падения равен углу отражения) ∠ОВС = ∠ОBА и ∠ОСВ = ∠ОСА.

Поэтому ∠ABC = ∠АСВ. Следовательно, центр О лежит на высоте AD, проведенной к стороне ВС. Положение точки В, в которую надо направить шарик, чтобы после отражения в В и С он прошел через точку А, можно фиксировать заданием угла ∠BOD = α.

OD = R cosα, BD = R sinα,

Имеем:

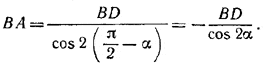
Так как ВО — биссектриса угла В в \(\Delta\)ABD, то

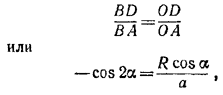
откуда для cosαполучаем уравнение

Решив его, найдем:

Второй корень отброшен, так как в силу R > а он дает значение cos α < — 1.

Если мы теперь предположим, что ∠АВС = 0, то получим второе решение задачи: точки В и С находятся на концах диаметра, проходящего через точку А.