В равносторонний треугольник со стороной а вписан круг. Затем в этот треугольник вписаны еще три круга, касающиеся первого круга и сторон треугольника, и еще три круга, касающиеся только что вписанных кругов и сторон треугольника, и т. д. Найти сумму площадей всех вписанных кругов ( то есть предел суммы площадей вписанных кругов.)

Центр О первого круга (рис.) делит высоту BN = h в отношении ВО : ОN = 2 : 1. Следовательно, диаметр MN составляет ²/₃ h и значит, ВМ = ¹/₃ h.

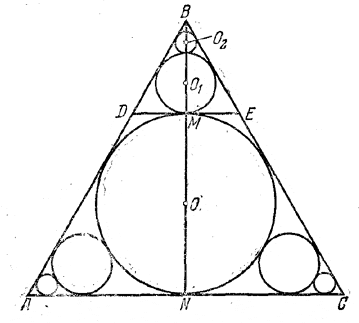
Второй круг вписан в треугольник DBE, высота кoторого втрое меньше высоты h треугольника ABC. Значит радиус r₁ = O₁ М втрое меньше радиуса r = ОN. Поэтому, если S есть площадь крута О то площадь крута О₁ будет А так как таких кругов три, то общая их площадь Q₁ будет

Q₁ = ¹/₃S

Рассуждая так же, найдем, что общая площадь трех следующих кругов будет

Получим бесконечный ряд слагаемых

Члены этого ряда, начиная с члена ¹/₃S (слагаемое S выделяется особо), образуют бесконечную убывающую геометрическую прогрессию Сумма этой прогрессии равна

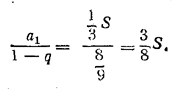
Сюда нужно еще прибавить слагаемое S.

Ответ: Искомая площадь равна ¹¹/₈ S = ¹¹/₉₆ πа²