Центр круга, вписанного в прямоугольную трапецию, отстоит от концов боковой стороны на 2 см и 4 см. Найти площадь трапеции.

Треугольники ОMC и ОND (рис.) подобны (см. предыдущую задачу).

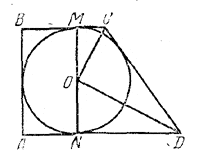
Так как ^OD/_OC = ⁴/₂ = 2 , ^ND/_OM = 2 и ^ON/_MC = 2 т. е. ND =2OM = 2r и МС =^ON/₂ = ¹/₂r. Из прямоугольного треугольника OND находим r² + (2r)² = 4², откуда

r = ⁴/_√5 (см)

Теперь находим AD = AN + ND = r + 2r = 3r = ¹²/_√5 см и BC = ⁶/_√5 см

Высота MN трапеции равна 2r = ⁸/_√5 см

Ответ: S = 14,4 см².