Около круга радиуса г описана прямоугольная трапеция, наименьшая из сторон которой равна ^3r/₂. Определить площадь трапеции.

Так как боковая сторона АВ (рис.), перпендикулярная к основаниям, равна 2r, то наклонная боковая сторона CD больше, чем 2r. Значит, наименьшая сторона трапеции, равная ³/₂ r, есть (меньшее) основание ВС.

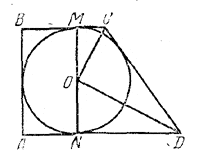
Чтобы найти большее основание AD, проведем прямые ОС и OD. Они являются биссектрисами углов MCD и NDC, в сумме составляющих 180°.

Следовательно, ∠MCO + ∠ODN = 90°. Из прямоугольного треугольника ODN находим ∠NOD + ∠ODN = 90°. Следовательно, ∠NOD = ∠MCO, так что треугольники ODN и ОСМ подобны. Получаем пропорцию ND : ON = OM : МС, где ON = OM= r и МС = ^r/₂ (по условию задачи). Отсюда ND = 2r, так что AD = AN + ND = r + 2r = 3r