В правильную треугольную призму вписан шар, касающийся трех граней и обоих оснований призмы. Найти отношение поверхности шара к полной поверхности призмы.

Высота призмы равна диаметру 2R вписанного шара. Если через центр О шара провести плоскость, параллельную основаниям призмы, то в сечении призмы получим равносторонний треугольник КLМ (рис.), равный основанию призмы, а в сечении шара - большой круг PNQ, вписанный в треугольник KLM.

Для наглядности рядом с рис. помещаем рисунок (а - наглядное изображение рассматриваемого тела.

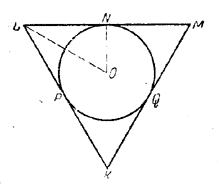
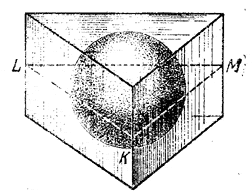
рис. рис. a

Из треугольника LON, где ON=R и ∠ NLO = 30°, найдем LN = R√3 . Следовательно, LM= а =2R√3. Боковая поверхность S_бок. призмы равна S_бок.= 3aH= 12R²√3. Площадь основания

Следовательно,

S_п. = 12R²√3 + 6R²√3 = 18R²√3

Поверхность же шара равна 4πR².

Ответ: Искомое отношение равно