В шар вписан конус, объем которого равен ¹/₄ объема шара. Найти объем шара, если высота конуса равна Н.

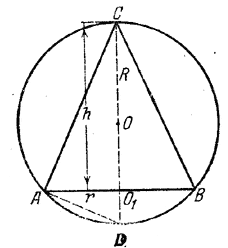
При обозначениях рис. объем шара равен ⁴/₃πR³, а объем конуса AСВ равен ¹/₃πr² • СО₁ = ¹/₃πr²H.

По условию

¹/₃πr²H = ¹/₄ •⁴/₃πR³

т. е. r²H = R³. Еще одну зависимость между r и R мы получим из прямоугольного треугольника CAD; именно, АО₁² =CO₁ • DO₁ т. е. r² = H (2R - Н). Подставляя это выражение в предыдущее равенство, получим R³ - 2H²R + H³= 0. Хотя это уравнение третьей степени относительно неизвестного R, но одно его решение R = H сразу усматривается (его можно было угадать и непосредственно по условию, так как конус, у которого радиус основания и высота равны радиусу шара, составляет по объему ¹/₄ шара). Следовательно (по теореме Безу), левую часть можно разложить на множители, один из которых равен R - H. Для этого достаточно разделить R³ - 2H²R + H³ на R - H или применить такое преобразование:

R³ - 2H²R + H³ = (R³ - H²R) - (H²R - H³) = R (R- Н) (R + H) - H²(R - H) =
=(R - H) (R²+ RH - H²)=0.

Уравнение R²+ RH - H² = 0 имеет один положительный корень

(отрицательный корень не годится).

Геометрически это означает, что радиус шара равен большей части высоты конуса, разделенной в крайнем и среднем отношении.

Ответ: Задача имеет два решения: V = ⁴/₃πH³ и V = ⁴/₃π (√5 - 2) H³.