Найти геометрическое место центров сечений шара плоскостями, проходящими через данную прямую l. Разобрать случаи, когда прямая пересекает шар, касается его или не имеет с ним общих точек.
Пусть О - центр данного шара. Проведем через данную прямую l некоторую плоскость Р, пересекающую сферу по окружности с центром в точке М.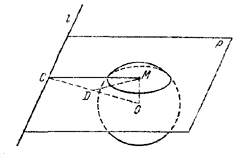
Как известно, ОМ ⊥Р. Проведем, далее, через точку О плоскость Р1, перпендакулярную к прямой l. Точку пересечения плоскости Р1 и прямой l обозначим через С. Так как плоскости Р1 и Р перпендикулярны, то отрезок ОМ содержится в плоскости Р1.
Рассмотрим теперь прямоугольный треугольник ОМС. Точка С не зависит от выбора секущей плоскости Р, и гипотенуза ОС прямоугольного треугольника ОМС есть величина постоянная. Если D - середина ОС, то MD = OC/2 . Следовательно, если l не имеет со сферой общих точек, то искомое геометрическое место есть часть дуги окружности радиуса OC/2 , заключенная внутри сферы (дуга лежит в плоскости P1 и проходит через центр сферы). Если l касается сферы, то искомое геометрическое место - окружность радиуса R/2 , где R - радиус сферы. Наконец, если l пересекает сферу, то геометрическое место точек М - окружность радиуса OC/2.