Найти геометрическое место проекций данной точки пространства на плоскости, проходящей через другую данную точку.

Пусть Р-одна из плоскостей, проходящих через данную точку A, а М - проекция данной точки В на плоскость Р. Пусть, далее, С - середина отрезка АВ.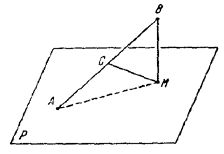

Так как треугольник АМВ прямоугольный, то СM = ¹/₂ АВ.

Таким образом, все точки М находятся от точки С на одном и том же расстоянии ¹/₂ АВ и, следовательно, расположены на сфере радиуса ¹/₂ АВ с центром в точке С. Легко видеть, кроме того, что любая точка указанной сферы совпадает с одной из проекций точки В. Таким образом, искомое геометрическое место есть сфера с диаметром АВ.