Даны две параллельные прямые и точка А между ними. Найти стороны прямоугольного треугольника, вершина прямого угла которого лежит в точке А, а вершины острых углов — на заданных параллельных прямых, зная, что площадь треугольника равна заданной величине k².

Обозначим через a и bрасстояния данной точки А от данных прямых l₁и l₂, а через х и у — длины катетов искомого треугольника (рис.).

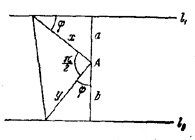
Заметив, что ^a/_x= sin φ, ^b/_y = cos φ, будем иметь два уравнения:

Преобразовав эти уравнения, придем к системе

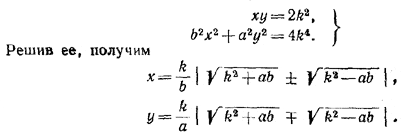
Задача разрешима при k² > ab и имеет два решения при k² > abи одно решение при k² =ab.