Внутрь правильного n-угольника со стороной а вписано п равных кругов так, что каждый круг касается двух смежных сторон многоугольника и двух других кругов, Найти площадь «звездочки», образующейся в центре многоугольника.
Соединив центры кругов, получим многоугольник, подобный данному. Центр полученного многоугольника совпадает с центром данного и стороны его соответственно параллельны сторонам данного (рис.).
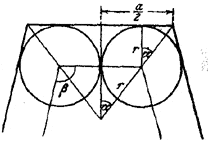
Пусть r — общий радиус рассматриваемых кругов. Тогда сторона построенного нами многоугольника равна 2r , а его площадь
б = nr2 ctg π/n
Пусть, далее, ![]() — внутренний угол многоугольника. Для
— внутренний угол многоугольника. Для
искомой площади S «звездочки» мы получаем выражение
![]()
Легко далее видеть (см. рис.), что
a/2 — r = r tg π/n
а откуда 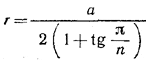 и, следовательно,
и, следовательно,
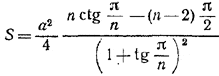
Похожие примеры: