Доказать, что прямая, пересекающая две грани двугранного угла, образует с ними равные углы тогда и только тогда, когда точки пересечения одинаково удалены от ребра.

Пусть Р и Q - точки пересечения данной прямой с гранями СВА и DBA двугранного угла (рис.).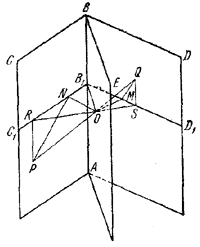

Проведем через ребро АВ биссекторную плоскость ABE, а затем через точку О ее пересечения с прямой PQ проведем плоскость C₁B₁D₁, перпендикулярную к ребру АВ. Пусть, далее, OM⊥B₁D₁, ON ⊥B₁C₁ и пусть SR- проекция PQ на плоскость D₁B₁C₁, так что при этом QS ⊥ B₁D₁, a PR ⊥ B₁C₁. Если точки P и Q одинаково удалены от ребра, т. е.

B₁R = B₁S, (1)

то треугольник B₁RS- равнобедренный, SO = RO и, следовательно, QO = PO как наклонные, имеющие равные проекции. Учитывая еще, что по построению

МО = NO, (2)

мы сможем заключить, что треугольники OMQ и ONP прямоугольные и равные. Отсюда следует равенство углов:

∠MQO = ∠NPO (3)

Итак, в одну сторону утверждение доказано.

Если, наоборот, выполнено равенство углов (3), то в силу (2) имеет место равенство треугольников QMO и PNO. Вследствие этого QO = PO и, значит, SO = OR. Отсюда уже следует равенство (1).