В пространстве рассматриваются два отрезка АВ и CD, не лежащих в одной плоскости. Пусть MN-отрезок, соединяющий их середины. Доказать, что \( \frac{AB + BC}{2} > MN \) (здесь AD, ВС и MN-длины соответствующих отрезков).

Соединим точки В и С, А и D отрезками прямых (рис.).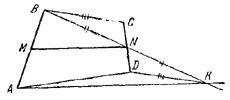

Через точку А проведем прямую параллельно MN до встречи в точке К с прямой, проходящей через В и N. Заметим, что AK = 2MN, так как MN - средняя линия в треугольнике АВК. Далее, \(\Delta\)BNC = \(\Delta\)KND, ибо BN = NK, CN=ND a ∠BNC = ∠KND. Поэтому DK = ВС. Из треугольника ADK следует:

DK + AD > AK=2MN

(здесь важно, что точка D не лежит на прямой АК, иначе пришлось бы поставить знак >). Итак,

BC+AD > 2MN,

что и требовалось доказать.