Доказать, что если в треугольной пирамиде все грани равновелики, то они равны.
Пусть DL и СМ - высоты треугольников ADB и АСВ, опущенные на общее основание АВ (рис.).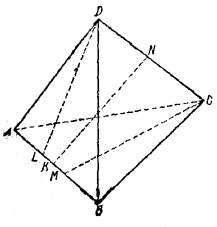
Так как эти треугольники равновелики, то DL= CM. Пусть еще KN-общий перпендикуляр к скрещивающимся ребрам АВ и DC. Проведем через отрезок КN плоскость Р, перпендикулярную ребру АВ. Четырехугольник LMCD спроектируем на плоскость Р (рис.).
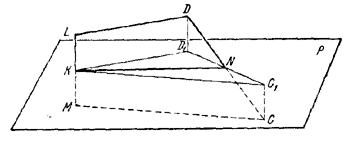
Так как отрезки DL и СМ проектируются без изменения длин (они параллельны плоскости Р), а отрезок LM- в точку, то в проекции получается равнобедренный треугольник KD1C1. По построению KN ⊥ DC, следовательно, KN ⊥ D1C1 и значит, KN - высота \(\Delta\)KD1C1. Поэтому N - середина отрезка D1C1, а значит, и отрезка DC.
Таким образом, в условиях задачи основание общего перпендикуляра к двум скрещивающимся ребрам пирамиды делит эти ребра пополам.
Из рис. 237 легко заметить, что LK = KM, ибо DD1 = CC1.
Поэтому (см. рис. вначале) AL = BM и из равенства прямоугольных треугольников ALD и ВМС следует, что
AD = BC.
Аналогично доказывается, что AC = BD и АВ = DC. Следовательно, все грани равны между собой, как треугольники, имеющие по три равные стороны.