На двух параллельных плоскостях расположены отрезки АВ и CD. Концы этих отрезков являются вершинами некоторой треугольной пирамиды. Доказать, что объем пирамиды сохраняется, если отрезки перемещать в этих плоскостях параллельно самим себе.

Пусть отрезок АВ лежит в плоскости Q, а отрезок CD - в плоскости Р и пусть Р || Q (рис.).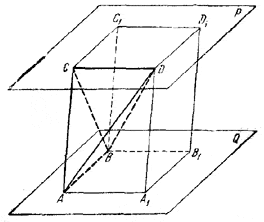

Проведем через точку А прямую, параллельную CD, и отложим отрезок AA₁ = CD. На сторонах АВ и АА₁ построим параллелограмм АВВ₁А₁. Аналогичное построение сделаем в плоскости Р. Соединив А с С, В с C₁ , А₁ с D и B₁ с D₁ , получим параллелепипед ABB₁A₁DCC₁D₁. Рассматривая грань АСВ в качестве основания пирамиды DACB, мы видим, что объем пирамиды равен ¹/₆ объема параллелепипеда. Так как, однако, объем параллелепипеда сохраняется при перемещении отрезков (не изменяются площадь основания АВВ₁А₁ и высота - расстояние между плоскостями Р и Q), то сохраняется и объем пирамиды.