Доказать, что если все двугранные углы некоторой треугольной пирамиды равны, то все ребра этой пирамиды также равны.

Пусть SABC-данная пирамида (рис.).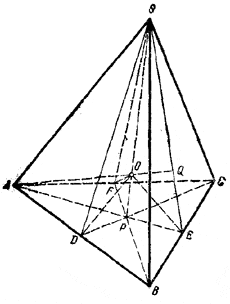

Опустим из вершины S на грань ABC высоту SP и проведем, кроме того, из той же вершины высоты SO, SE и SF остальных трех граней. Легко видеть, что треугольники SPD, SPE и SPF в силу равенства углов SDP, SEP и SFP равны между собой.

Проведем далее через ребра АВ, ВС и АС плоскости, делящие соответствующие двугранные углы пополам. Эти плоскости пересекаются в точке О, равноудаленной от всех четырех граней пирамиды и, следовательно, являющейся центром вписанного в пирамиду шара. Легко видеть, что в рассматриваемом случае в силу отмеченного равенства треугольников точка O окажется на высоте пирамиды SP. Повторяя рассуждения, мы установим, что все высоты пирамиды пересекаются в точке О. Используя этот факт, мы можем утверждать, что, например, треугольники APS и SPE лежат в одной плоскости и, следовательно, отрезки АР и РЕ расположены на одной прямой. Поэтому АЕ есть одновременно биссектриса и высота \(\Delta\)ABC. По аналогичной причине и остальные биссектрисы \(\Delta\)ABC являются его высотами. Следовательно, \(\Delta\)ABC равносторонний. Повторяя рассуждение, мы установим, что все грани пирамиды представляют собой равносторонние треугольники, что и завершает доказательство.