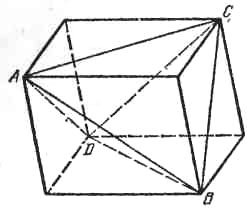
Из того, что ребра пирамиды ABCD касаются шара, следует, что суммы противоположных ребер пирамиды равны. Достроим пирамиду ABCD до параллелепипеда, проведя через каждое ребро пирамиды плоскость, параллельную противоположному ребру. Ребра пирамиды будут являться диагоналями граней параллелепипеда (рис.), а ребра параллелепипеда равны расстояниям между серединами противоположных ребер пирамиды. Пусть |AD| = a, |ВС| = b, тогда любые два противоположных ребра пирамиды будут равны a и b.

Докажем это. Пусть |АВ| = x, |DC| = y. Тогда х + у = a + b, х² + y² = а² + b² (последнее равенство следует из того, что все грани параллелепипеда - ромбы с равными сторонами).

Отсюда следует, что х = а, у = b или x = b, у = а. Значит, в ΔАВС по крайней мере две стороны равны между собой. Но ∠AВС = 100°, следовательно, |АВ| = х = |ВС| = b, |АB| = а, |DB| = b, |DC| = а.

Из ΔAВС найдем а = 2b sin 50°,

$$ V_{ABCD}=\frac{1}{3}S_{ADC}h_B = \frac{1}{3}\cdot\frac{a^2\sqrt3}{4}h_B =\\=\frac{1}{3}S_{DBC}h_A = \frac{1}{3}\cdot\frac{b^2sin100°}{2}h_A $$

откуда

$$ \frac{h_A}{h_B}=\frac{a^2\sqrt3}{2b^2sin100°}=\sqrt3tg50° $$