Равенство произведений длин ребер при каждой грани означает, что противоположные ребра пирамиды равны. Достроим пирамиду SABC обычным образом до параллелепипеда, проведя через каждое ребро плоскость, параллельную противоположному ребру. Ввиду равенства противоположных ребер пирамиды SABC, получившийся параллелепипед будет прямоугольным. Обозначим ребра этого параллелепипеда через a, b и c, как показано на рис.

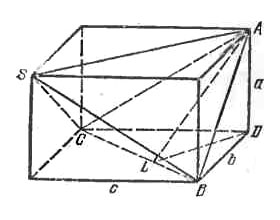
Проведем в ΔBCD высоту DL. Из ΔBCD найдем

$$ |DL|=\frac{bc}{\sqrt{b^2+c^2}},\\|AL|=\sqrt{a^2+|DL|^2}=\frac{\sqrt{a^2b^2+b^2c^2+c^2a^2}}{\sqrt{b^2+c^2}},\\ S_{ABC}=\frac{1}{2}\sqrt{a^2b^2+b^2c^2+c^2a^2} $$

Объем пирамиды SABC составляет 1/3 объема параллелепипеда, высота на грань АВС дана, получаем уравнение

$$ \sqrt{a^2b^2+b^2c^2+c^2a^2}\cdot\sqrt{\frac{102}{55}} = abc \;\;\;\;\;\;(1) $$

По теореме косинусов для ΔАВС получим

$$ 6a^2=\sqrt{a^2+c^2}\cdot\sqrt{a^2+b^2}\cdot\sqrt{\frac{17}{2}}\;\;\;\;\;\;(2) $$

И, наконец, последнее условие задачи даст нам

$$ c^2-2a^2-2b^2=30\;\;\;\;\;\; (3)$$

Решив систему (1)-(3), найдем а² = 34, b² = 2, с² = 102.

Ответ: \(\frac{34\sqrt6}{3}\)