Доказать, что всякая плоскость, проходящая через середины двух противоположных ребер тетраэдра, делит этот тетраэдр на две равновеликие части.

Пусть SABC - данный тетраэдр, Р и Q - середины противоположных ребер АС и SB, MPNQ - некоторое сечение тетраэдра, содержащее отрезок PQ (рис.).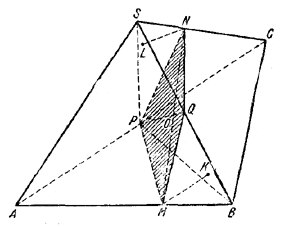

Рассмотрим плоское сечение SPB, которое, очевидно, разбивает тетраэдр на две равновеликие части. Задача будет решена, если мы докажем, что пирамиды SPQN и MPQB равновелики.

Опустим на плоскость SPB перпендикуляры из точек М и N и их основания обозначим соответственно через К и L. Так как треугольники PQB и SPQ равновелики, то для решения задачи достаточно показать, что LN = MK. Мы установим это равенство, доказав, что

MO = NO. (1)

Рассмотрим с этой целью пару параллельных плоскостей, в которых лежат скрещивающиеся прямые SC и АВ (рис.).

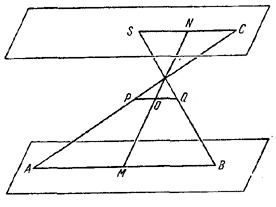
Так как отрезок PQ соединяет середины отрезков АС и SB, то он, очевидно, лежит в плоскости, параллельной данным плоскостям и отстоящей от них на равном расстоянии. В силу этого отрезок MN, пересекаясь с отрезком PQ, разделится точкой пересечения пополам.