Показать, что если плоскость, проведенная через концы трех ребер параллелепипеда, исходящих из одной вершины, отсекает от параллелепипеда правильный тетраэдр, то параллелепипед можно пересечь плоскостью так, чтобы в сечении получился правильный шестиугольник.

Проведем указанную в задаче плоскость через вершины B, D, F (рис.) и параллельную ей плоскость через вершины C, Е, G.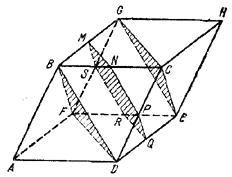

Обе плоскости образуют в пересечении с параллелепипедом равносторонние и равные треугольники. Длину стороны каждого из этих треугольников обозначим через a. Если теперь, через середину одного из шести ребер, соединяющих вершины двух указанных треугольников, например через середину N ребра ВС, - провести плоскость, параллельную двум указанным плоскостям, то она даст в сечении с параллелепипедом шестиугольник MNPQRS, все стороны которого, очевидно, окажутся равными ^a/₂ . Заметим еще, что MN || DF и NP || BD. Поэтому ∠MNP дополняет ∠BDF до 180° и, следовательно, ∠MNP = 120°. Аналогично устанавливаем, что и остальные углы шестиугольника равны 120°.