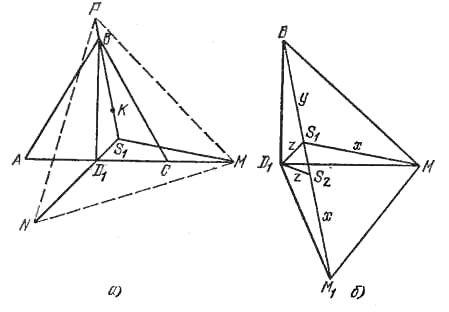
Спроектируем данные многогранники на плоскость АВС. На рисунке не показаны проекции точек А₁, В₁ и С₁ - они совпали с точками А, В и С; S₁ и D₁ - проекции точек S и D. Если мы на отрезке PS₁ возьмем точку К так, что |РК| = |ND₁|, то точка К является проекцией точки в которой ребро PS пересекает плоскость A₁B₁C₁. Таким образом, искомое отношение равно

$$\frac{|KB|}{|BP|}=\frac{|ND_1|-|PB|}{|PB|}=\\=\frac{(|S_1N|-|D_1S_1|)-(|PS_1|-|BS_1|)}{|PS_1|-|BS_1|}=\frac{|BS_1|-|D_1S_1|}{|S_1M|-|BS_1|} \;\;\;\;\;\;\;\;\;(1)$$

Следовательно, задача сводится к нахождению отрезков |S₁M|, |BS₁|, |D₁S₁|, где S₁ - точка, из некоторой стороны ΔBD₁M видны под равными углами, ΔВD₁М - прямоугольный с катетами |D₁M| = 2а, |BD₁| = a√3.

Обозначим |S₁M| = x, |S₁B| = у, |S₁D₁| = z.

Повернем ΔD₁S₁M на угол 60° вокруг точки D₁ (рис., б), ΔD₁S₁S₂ - правильный со стороной z; точки В, S₁, S₂, M₁ - на одной прямой, ∠BD₁M₁ = 150°. Из ΔBD₁M₁ найдем х + у + z = а√13. Высота ΔBD₁M₁, опущенная на сторону ВМ₁, равна

$$a\sqrt{\frac{3}{13}}$$ откуда $$z = \frac{2a}{\sqrt{13}},\;\;y+\frac{z}{2}=\sqrt{3a^2-\frac{3a^2}{13}}=\frac{6a}{\sqrt{13}}$$

Теперь легко найти $у = \frac{5a}{\sqrt{13}},\;\;х =\frac{6a}{\sqrt{13}}$. Подставляя найденные значения в (1), получим, что искомое отношение, считая от вершины В, равно 3.