Доказать, что две плоскости, проведенные через концы двух троек ребер параллелепипеда, исходящих из концов диагонали параллелепипеда, рассекают эту диагональ на три равные части.

Рассмотрим две плоскости, заштрихованные на рис., и треугольник ADE в плоскости Р, проходящей через вершины A, D, Н, Е данного параллелепипеда.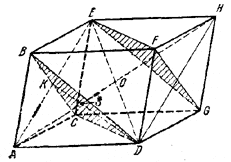

Плоскость Р пересекает плоскость \(\Delta\)BCD по прямой KD, которая проходит через точку К пересечения диагоналей параллелограмма АВЕС, и следовательно, отрезок KD есть медиана \(\Delta\)AED. Очевидно, что АР есть также медиана \(\Delta\)AED. Поэтому интересующая нас точка S есть точка пересечения медиан \(\Delta\)AED и, значит,

AS = ²/₃AО = ¹/₃AH,

что и требуется.