Два равных треугольника \(\Delta KLM\) и \(\Delta KLN\) имеют общую сторону KL, ∠KLM = ∠LKN = π/3, |KL| = a, |LM| = |KN| = 6c. Плоскости KLM и KLN взаимно перпендикулярны. Шар касается отрезков LM и KN в их серединах. Найти радиус шара.
Пусть O1 и O2 - проекции центра шара О на плоскости KLM и KLN, Р - середина ML.
Проекции O1 и O2 на KL должны совпадать. Можно доказать, что эти проекции попадают в середину KL - точку Q (рис.).
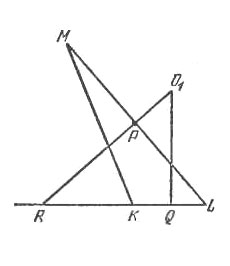
Если мы продолжим O1Р до пересечения с прямой KL в точке R, то из прямоугольного треугольника \(\Delta PLR\) найдем |RL| = 6а, |RP| = 3a√3. Затем найдем
$$ |RQ|=\frac{11a}{2},\;\;|O_1Q|=\frac{11a\sqrt3}{6},\;\;|RO_1|=\frac{11a\sqrt3}{3} \\ |PO_1|=\frac{11a\sqrt3}{3}-3a\sqrt3 = \frac{2a\sqrt3}{3} $$Следовательно, радиус сферы равен
$$ \sqrt{\frac{4a^2}{3}+\frac{121a^2}{12}} = \frac{a}{2}\sqrt{\frac{137}{3}} $$Похожие примеры: