В правильном тетраэдре SABC с ребром основания а проведены три плоскости, каждая из которых проходит через одну из вершин основания тетраэдра ABC и середины двух боковых ребер. Найти объем части тетраэдра, расположенной над всеми секущими плоскостями.

Рассматриваемое тело составлено из двух пирамид с общим основанием KMN.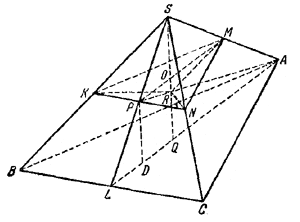

Высоту OR нижней пирамиды легко найти, опустив из точки Р (середины стороны KN) перпендикуляр PD на основание пирамиды. Точка D при этом разделит отрезок QL пополам. Используя этот факт, из \(\Delta\)APD получаем:

^PD/_RQ = ^DA/_QA = ⁵/₄

Отсюда RQ = ⁴/₅PD, и, следовательно,

Мы воспользовались здесь тем, что в правильном тетраэдре высота равна
Искомый объем равен