В прямоугольном параллелепипеде ABCDA1B1C1D1 длины ребер АВ, ВС и ВВ1 равны соответственно 2a, a и a, точка Е - середина ребра ВС. Вершины М и N правильного тетраэдра MNPQ лежат на прямой С1Е, вершины Р и Q - на прямой, проходящей через точку B1 и пересекающей прямую AD в точке F. Найти: а) длину отрезка DF; б) расстояние между серединами отрезков MN и PQ.
Поскольку противоположные ребра правильного тетраэдра перпендикулярны, перпендикулярными должны быть прямые С1Е и B1F (рис.).
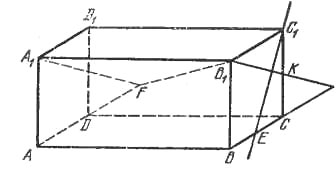
Если К - середина С1С, то, поскольку прямые В1К и В1А1 перпендикулярны прямой С1Е, прямая B1F должна лежать в плоскости, проходящей через В1К и В1А1, а отсюда следует, что A1F||В1К и, значит, |DF| = a (это ответ на пункт а)).
б) Расстояние между серединами MN и PQ равно расстоянию между прямыми B1F и С1Е. Его можно найти, приравнивая различные выражения для объема тетраэдра FВ1С1Е:
$$ \frac{1}{3}S_{B_1C_1E}2a = \frac{1}{6}|FB_1|\cdot|C_1E|\cdot x $$Отсюда \(x=\frac{4a}{3\sqrt5}\)
Похожие примеры: