Сторона основания правильной четырехугольной пирамиды равна а, высота пирамиды h. Через сторону основания пирамиды и середину скрещивающегося с ней бокового ребра проведено сечение. Определить расстояние от вершины пирамиды до плоскости этого сечения.

Пусть AEFD - получающаяся в сечении равнобочная трапеция и пусть G и Н - середины ее оснований.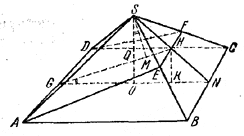

Опустим из точки Н перпендикуляр НК на основание пирамиды. Так как Н-середина SN, то

HK = ^h/₂, KN = ^a/₄, GK= ^3a/₄. (1)

Определим, далее, длины отрезков QO и QS. Так как

^QO/_HK = ^GO/_GK'

то, учитывая (1), получаем

Отсюда QS = ²/₃h,

(2)

Опустим из точки S перпендикуляр SM на GH. Тогда из подобия треугольников SMQ и GOQ имеем

^SM/_QS = ^GO/_GQ

и, следовательно, искомое расстояние равно