Основанием пирамиды SABCD является ромб с диагоналями AC = a, BD = b. Боковое ребро SA перпендикулярно плоскости основания и равно q. Через точку А и середину К ребра SC проведена плоскость, параллельная диагонали основания BD. Определить площадь сечения.

Пусть AMKN - четырехугольник, получающийся в сечении, и Q - точка пересечения его диагоналей.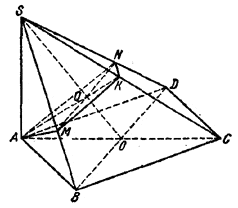

Рассматривая \(\Delta\)SAC, легко заметить, что Q лежит на пересечении медиан этого треугольника. Поэтому

^MN/_BD = ^SQ/_SO = ²/₃

и значит, MN = ²/₃ b. Далее из прямоугольного треугольника SAC находим

AK = ¹/₂SC = ¹/₂√q²+ a²

Так как АК ⊥ MN, то

S_сеч. = ¹/₂ АК•MN= ^b/₆ √q²+ a²