На отрезке длины 2а + 2b и его частях длины 2а и 2b как на диаметрах построены полуокружности, лежащие по одну сторону от отрезка. Найти радиус окружности, касающейся трех построенных полуокружностей.

Пусть О₃D ⊥ О₁О₂(см. рис.).

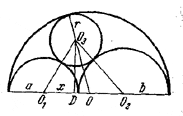
Имеем

OO₃² = O₁O₃²+ O₁O²— 2O₁O • O₁D = O₂O₃²+ OO₂² —2OO₂ • DO₂, (1)

где O₁O₃ = a+ r, O₂O₃ = b+ r, O₁O = (а + b)— а = b, OO₂ = (а + b) — b = a.

Положив O₁D = x, запишем второе равенство (1) в такой форме:

(a+ r)² + b²— 2bx = (b+ r)² + a²—2а (а + b — х),

откуда найдем, что

Теперь первое равенство (1) примет вид уравнения с одним неизвестным r

Решив это уравнение, окончательно получим