В прямоугольный треугольник вписан полукруг так, что диаметр его лежит на гипотенузе и центр его делит гипотенузу на отрезки, равные 15 см и 20 см. Определить длину дуги полукруга, заключенной между точками касания его с катетами.

Так как углы В, D и E четырехугольника ODBE прямые и DO = OE, то этот четырехугольник есть квадрат.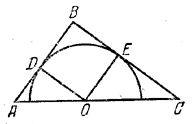

Искомая дуга DE равна четверти длины всей окружности. Обозначим ее радиус через R. Из подобия треугольников ADO и ОЕС имеем

^АD/_AO = ^OE/_OC

Так как

AD = √АО² - OD²= √15² - R²,

то

Отсюда R = 12.

Отв. 6π.