Из точки, отстоящей от центра круга на m см, проведены касательные к кругу. Расстояние между точками касания равно a см. Определить радиус круга.
Задача сводится к нахождению одного из катетов треугольника ОАВ по данной гипотенузе OА = m и высоте BD = a/2.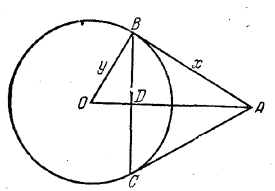
Обозначим больший катет через x меньший - через y. Двоякое выражение площади треугольника ОАВ (см. решение задачи 276) дает уравнение
xy = а m/2, т. e. 2xy = am;
кроме того, x2 + у2 = m2. Складывая и вычитая эти уравнения почленно, получим
x + y= √m2+ am
и
x - у = √m2- am
Как x, так и yможет служитm искомым радиусом.
Отв. 1/2(√m2+ am + √m2- am) или 1/2 (√m2+ am - √m2- am).
Похожие примеры: