Может ли быть правильным треугольник, расстояния вершин которого до двух данных взаимно перпендикулярных прямых выражаются целыми числами?

Проведем через вершину А данного \(\Delta\)ABC прямую AD, параллельную одной из данных прямых х и у и не пересекающую треугольник, и опустим из точек В и С перпендикуляры ВР и CQ на AD.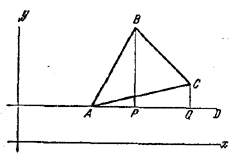

Предположим, что расстояния вершин треугольника ABC от прямых х и у выражаются целыми числами. Тогда длины отрезков АР, AQ, ВР, CQ также будут выражаться целыми числами. В силу этого

будут числами рациональными, а значит, будет рациональным и число

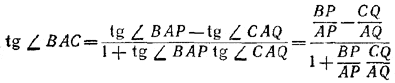
Поэтому невозможно, чтобы ∠ВAС = 60°, так как tg 60° = √3 есть число иррациональное. Следовательно, \(\Delta\)ABC не может быть правильным.