В точках А и В прямой, по одну сторону от нее, восставлены два перпендикуляра АА₁ = а и ВВ₁ = b. Доказать, что при сохранении величин а и b точка пересечения прямых АВ₁ и А₁В будет находиться на одном и том же расстоянии от прямой АВ независимо от положения точек А и В.

Пусть прямые А₁В и АВ₁ пересекаются в точке О и OD ⊥ AB.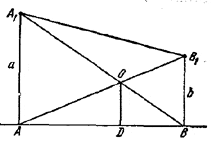

Так как \(\Delta\)АВА₁ ~ \(\Delta\)DBO и \(\Delta\)ВАВ₁ ~ \(\Delta\)DАО, то

Отсюда

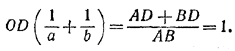
Следовательно, расстояние

не зависит от положения точек А и В (при сохранении величин а и b).