В прямой угол с вершиной А вписана окружность; В и С — точки касания. Доказать, что если к данной окружности провести касательную, пересекающую стороны АВ и АС в точках М и N, то она отсечет на этих сторонах отрезки MB и NC, сумма длин которых больше, чем ¹/₃(АВ + АС), и меньше, чем ¹/₂ (АВ + АС)

Если K — точка касания отрезка MN с окружностью,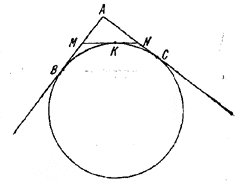

то ВМ = МК, KN = NC, откуда

MN = BM + CN. (1)

Ho MN < AM + AN. Поэтому

2MN < BM + AM + CN + AN = AB + AC,

откуда

С другой стороны, MN > AN и MN > AM, так как MN — гипотенуза в треугольнике AMN. Поэтому 2MN > AN + AM и, в силу (1), 3MN > AN + NC+ AM + МВ = АВ + АС.

Следовательно,